Danny Milosavljevic
Dieses Dokument verwendet „.“ als Dezimalpunkt. Zahlen werden in E-Notation geschrieben: 3.5E4 ist eine Abkürzung für 3.5⋅10**4. Winkel sind in Radiant, außer es steht das Zeichen „°“ nach der Zahl - dann ist die Zahl in Graden.
Der Satellit INTERCOSMOS 24 untersucht die Ausbreitung von ELF-Wellen an der Magnetosphäre. Federführend war die Tschechische Republik, im Rahmen von Projekt „Aktivny“. Außerdem beteiligt waren Bularien, Deutschland, Ungarn, Polen, Rumänien.
Dazu emittiert ein anderer Satellit, Magion-2, elektromagnetische Wellen auf die Magnetosphäre.
Der Satellit INTERCOSMOS 24 hat einen Durchmesser von 20m, ein Gewicht von ca. 450kg.
Er hat folgende Apparate zur Messung der Auswirkung der Ionisierung von Gas bzw. Plasma bei Transmission von EM-Wellen:
0.30 bis 22kHz Empfänger für Niederfrequenz
0.10 bis 10MHz Plasmawellenspektrometer (30 bis 700keV)
KM-6 Langmuirplasmaanalyse: Messung von Elektron-Ion-Plasma-Temperatur und -Dichte.
NAM-05 zur Messung der Masse bzw. Dichte des Plasmas.
Das Two-Line-Element-Set des Satelliten ist:
1 20261U 89080A 10139.39358310 .00000127 00000-0 38124-4 0 1648
2 20261 82.5949 242.1254 1213683 287.9675 59.2974 12.53483797941704
Das bedeutet:
ω:=287.9675° (Argument of perigee – d.h. wo ist das Perigäum, wie ist die Ellipse in der Ebene gedreht)
BSTAR_drag=3.8124E-05
classification=U
n̈:=0.0
ṅ:=2⋅1.27E-06≈0
e:=0.1213683 (Exzentrizität)
element_number=164
epoch_day_of_year=139.3935831 (base 1)
epoch_year=10
i:=82.5949° (inclination: prograder orbit, von West nach Ost, beinahe polar)
launch_number_of_year=80
launch_piece=A
launch_year=89
χ:=59.2974° (mean anomaly)
revolution_number=94170 (base 1)
revolutions_per_day=12.53483797
Ω:=242.1254° (right ascension, vom Frühlingspunkt weg)
satellite_number=20261
d.h. der Satellit hatte die Erde zum Referenzzeitpunkt 94169 Mal vollständig umrundet.
T=(60⋅24)/revolutions_per_day≈114.88 min
Das SGP24-Modell, das dem Two-Line-Element-Set zugrunde liegt, ist auf ca. 1km genau.
Die Day-of-Year-Angabe 139.3935831 beginnt mit Tag Nummer 1.
Der Januar ist 31 Tage lang, der Februar 2010 ist 28 Tage lang, der März ist 31 Tage lang, der April ist 30 Tage lang, der Mai ist 31 Tage lang.
Das übliche Datumsformat gibt den Tag immer innerhalb des Monats an, daher versuchen wir, die Tagesnummer soweit runterzukriegen, dass sie in einen Monat zeigt:
139, zu groß, d.h. nach Januar.
139-31=108, zu groß, d.h. nach Februar.
108-28=80, zu groß, d.h. nach März.
80-31=49, zu groß, d.h. nach April.
49-30=19, okay, d.h. im Mai, Tag Nummer 19.
Für die Uhrzeit:
0.3935831 gibt den Anteil des Tages an, d.h. wieviel von 86400 Sekunden/Tag vergangen ist.
Daher: s:=0.3935831⋅86400=34005.57984 Sekunden des Tages sind vergangen.
Üblicherweise gibt man das getrennt in Stunden, Minuten, Sekunden an.
Daher versucht man, von den Gesamtsekunden s eine Maximalanzahl Stunden abzuziehen, sodass das Ergebnis immer noch >=0 ist. Da in UTC alle Minuten gleich lang sind und alle Sekunden gleich lang sind und diese bei 0 zu zählen anfangen, geht das einfacher durch Ganzzahldivision (//):
s//(60⋅60)=9 Stunden
R:=(s-9⋅60⋅60)=1605 Restsekunden
R//60=26 Minuten
R-26⋅60=45 Sekunden
t_0=2010-05-19T09:26:45Z
Das entspricht in Ortszeit Wien (derzeit zwei Stunden später als UTC):
t_0=2010-05-19T11:26:45 CEST
Zwei Himmelskörper (1 und 2) beeinflussen sich (hauptsächlich) durch die Gravitationskraft:
F=(G⋅m_1⋅m_2/r³)⋅r
Wobei G:=6.6E-11 m³/(kg⋅s²) die Gravitationskonstante ist.
Also bewegen sie sich wie folgt:
I) m_1⋅r̈_1=G⋅m_1⋅m_2⋅r/r³
II) m_2⋅r̈_2=-G⋅m_1⋅m_2⋅r/r³
mit r:=r_2-r_1
Addition ergibt:
m_1⋅r̈_1+m_2⋅r̈_2=G⋅m_1⋅m_2⋅r/r³-G⋅m_1⋅m_2⋅r/r³
m_1⋅r̈_1+m_2⋅r̈_2=0
Subtraktion von Gleichung II und Gleichung I nach Division durch die Massen ergibt:
r̈_2-r̈_1=-G⋅(m_1+m_2)⋅r/r³
Mit der Abkürzung μ:=G⋅(m_1+m_2) ergibt das für die Relativbewegung der Massen:
r̈=-μ⋅r/r³
Der Massenmittelpunkt (hier nicht gezeigt) bewegt sich immer gleichförmig.
Nach Multiplikation mit ṙ erhält man:
r̈⋅ṙ=-μ⋅r⋅ṙ/r³
Da gilt
r̈⋅ṙ=(d(ṙ²/2))/dt
folgt:
r̈⋅ṙ=-μ⋅ṙ/r²
(d(ṙ²/2))/dt=-μ⋅ṙ/r²
(d(ṙ²/2))/dt=μ⋅d(1/r)/dt
d(ṙ²/2-μ⋅1/r)/dt=0
Und damit nach Integration nach t:
∫d(ṙ²/2)-μ⋅∫d(1/r)=0
ṙ²/2-μ/r=C
Ein künstlicher Satellit beeinflusst den Planeten nur unmerklich, daher werden wir im folgenden immer nur die Kraft der Erde auf den Satelliten (Masse m, Position r) beachten:
μ=G⋅M_e≈6.67300E-11⋅5.9736E24=398618.33E9 m³/s²
Selbst Abweichungen von 600 Mio. kg hätten nur Auswirkungen in der 8. Nachkommastelle.
Da sich ein Körper in einem Zentralfeld immer in derselben Ebene befindet, identifizieren wir diese Ebene mit dem Normalvektor L:
L=r⨯p
L=m⋅(r⨯v)
L=m⋅(r⨯ṙ)
Daher auch |L|=const.
Legt man das Koordinatensystem praktischerweise genau so, dass die xy-Ebene diese Ebene ist, dann folgt (mit den üblichen Koordinatentransformationen für Polarkoordinaten x:=r⋅cos φ, y:=r⋅sin φ) durch einsetzen:
L=m⋅r²⋅φ̇=const
Bzw. einfacher:
r²⋅φ̇=const
Daher ist weiter weg die Winkelgeschwindigkeit des Satelliten um den Planeten kleiner als nahe am Planeten.
Da mit Two-Line-Elements nur elliptische Orbits dargestellt werden können (und e<1), ist der Orbit elliptisch.
Große Halbachse: a=(μ⋅T²/(2⋅π)²)**(1/3)
a≈7828km
apogee=2400.1km
perigee=699.63km
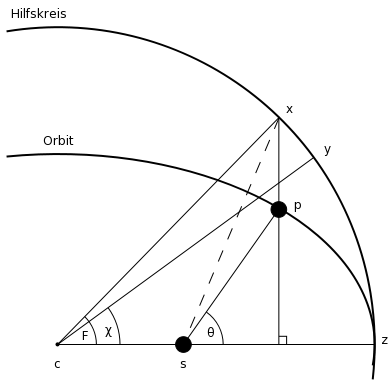
Die elliptische Bahn wird um einen Umkreis als Hilfskreis erweitert, der Winkel F wird vom Mittelpunkt dieses Hilfskreises aus gemessen (statt wie θ bei der Ellipse vom Brennpunkt aus).
y ist hier ein fiktiver Himmelskörper, der
dieselbe Umlaufzeit hat, aber mit konstanter
Winkelgeschwindigkeit rotiert.
Es folgt dann aus dem 2. Keplerschen Gesetz (Flächensatz):
F-e⋅sin F=τ_1
T=2⋅π⋅√(a³/μ)
χ=(2⋅π/T)⋅(t_0-t_P)
τ_1=(√(μ/a³))⋅(t_1-t_0)+χ≈788.654
Wenn t_1 10 Tage nach t_0 ist, dann ist der Wert für F ungefähr (ermittelt über Newtonsches Näherungsverfahren, siehe „newton_kepler.py“):
F≈788.6
bzw. normiert auf einen Bereich [0, 2⋅π):
F≈3.2018
Die wahre Anomalie θ kann aus F berechnet werden:
tan θ/2=(√((1+e)/(1-e)))⋅tan F/2
θ≈-3.0882627
Die Entfernung des Satelliten ist dann:
r=a⋅(1-e²)/(1+e⋅cos θ)
r≈8776km
Die geographische Breite ist dann:
sin B=(sin(ω+θ))⋅sin i
B≈1.1826
B≈67.76°
Wenn man die Erde näherungsweise als Kugel betrachtet und die Nähe des Breitengrades zur Antarktis berücksichtigt (d.h. die Erde als kleine Kugel mit Radius 6356.77km betrachtet), dann ist die Höhe h≈r-6356km≈2420km.
Wenn man es noch genauer haben will und die Erde als Ellipsoid betrachtet mit kleiner Halbachse 6356.77km und großer Halbachse 6378km (siehe „geoid.py“), dann ist die Höhe h≈r-6359799m≈2416km.
Die J_2-Störung (Jeffrey-Konstante 2) der Erde beträgt laut IERS 1.0826359E-3. Alle anderen Jeffrey-Konstanten sind vernachlässigbar klein.
Die Legendre-Polynome haben die erzeugende Funktion:
P_l^m(x):=(1/(2**l⋅l!))⋅d**l ((x²-1)**l)/dx**l
Das zweite Legendre-Polynom für (cos i) als Argument beträgt:
P_2(cos i)=(1/2)⋅(3⋅(cos i)²-1)
Damit wird die
Perigäumsdrehung:
Ω̇=-(3/2)⋅μ⋅J_2⋅(r_E²/(n⋅a**5))⋅(1-e²)**-2⋅cos
i
ω̇=(3/4)⋅n⋅a_E²⋅(5⋅(cos i)²-1)/(a²⋅(1-e²)²)⋅J_2
bzw.
ω̇=(3/2)⋅μ⋅J_2⋅(r_E²/(n⋅a**5))⋅(1-e²)**-2⋅(2-(5/2)⋅(sin i)²)
χ̇=(3/2)⋅μ⋅J_2⋅(r_E²/(n⋅a**5))⋅(1-e²)**(-3/2)⋅(1-(3/2)⋅(sin i)²)
χ̇=(3/2)⋅((J_2⋅r_E²)/(p_0²))⋅n_0⋅(1-e_0**2)**(1/2)⋅(1-(3/2)⋅(sin(i))**2)
mit n=n_0=(μ/a³)**1/2 (als konstant angenommen!)
und p_0=a_0⋅(1-e²)
bzw. in diesem Fall:
Ω̇≈1.30468924159E-07
ω̇≈-4.64110821704E-07
χ̇≈-4.774184530567762e-07
nach 10 Tagen daher:
ΔΩ≈0.1127
Δω≈-0.4010
Δχ≈-0.412
Damit folgt dann:
F≈2.8467
θ≈165.02°
Die Entfernung des Satelliten ist dann:
r=a⋅(1-e²)/(1+e⋅cos θ)≈8737056m
Die geographische Breite ist dann:
sin B=(sin(ω+Δω+θ))⋅sin i
B≈68.74°
Die Höhe ist dann:
h=r-6359549m≈2377507m≈2378km
Siehe auch „satellite.py“, Funktion „update“.
Referenzen
Wolfgang Steiner, Martin Schagerl – Dynamik und Steuerung von Raumfahrzeugen
http://www.geocities.co.jp/Technopolis/4025/Intercosmos.html#1
www.amsat.org/amsat/ftp/docs/spacetrk.pdf